Новый подход к формированию количественной оценки качества образования с позиций теории виртуального познания - В.В. Котенко, Д.В. Котенко, С.В. Поликарпов

,                                                    (1)

где  и   - двумерные спектральные плотности функций - V(x, у) и шума квантования, соответственно; 0  и 0 - пространственные частоты.

Минимизация данного выражения предполагает решение вариационной задачи, состоящей в определении экстремальной спектральной плотности шума квантования при следующих условиях:

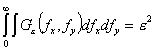,                                                                       (2)

                                                                          (3)

Решение в (1) данной вариационной задачи для случая, когда функция  является гауссовской и характеризуется экспоненциальным законом

изменения корреляции , приводит к параметрической системе двух уравнений:

                                                 (5)

где - дисперсия,  - величина кванта спектра познания.

Система уравнений (5) решается исключением параметра  числовым способом. В результате получается искомая зависимость эпсилон-энтропии на квант познания емкостью  от заданного среднего квадрата ошибки  формирования информационного обучения (рис.2).

Если задаться временем, отводимым на изучение кванта познания емкостью , и разделить на это время значения , то можно получить зависимость минимальной скорости обучения от заданного среднего квадрата ошибки формирования ИПО, то есть от заданного качества образования. Ввиду однозначной зависимости  и  график рис. 2 можно инвертировать и получить из него зависимость качества образования от скорости обучения. Таким образом, открывается возможность формирования количественной оценки качества образования.