Рассмотренные ранее особенности цифрового представления непрерывного источника S подсказывает, что энтропия H[X] может изменяться во времени, а так же сильно зависит от параметров дискретизации, квантования и кодирования. При информационном анализе цифрового представления эта проблема решалась путем введения понятия эпсилон-энтропия, которое характеризует минимальное среднее количество информации, необходимое для восстановления непрерывного сообщения с заданной точностью эпсилон (). Применив этот подход, выражение (6) можно преобразовать к виду:

(7)

где:- эпсилон-энтропия квантования;- максимальные потери цифрового представления, допустимые при заданной точности Подставив (7) в (4) получим:

(8)

    Условная энтропия H[S/X] в выражении (8) не зависит от используемого кода f. Это дает основание применить для оценки эффективности кодирования f непрерывных источников более удобного в практическом отношении характеристику, которая может быть получена из (8) следующим образом:

(9)

     Назовем эту характеристику относительной избыточностью кодирования f непрерывного источника при заданной точности цифрового представления . Нетрудно заметить, что выражение (9) справедливо только для случая, если сообщения источника являются непрерывными случайными величинами. Обобщение его для случая случайных процессов позволяет прийти к выражению вида:

(10)

где: - эпсилон-энтропия случайного процесса, для определения которой в зависимости от вида реального источника могут использоваться ранее полученные выражения [1]; - стоимость кодирования, которая в случае стационарного источника и постоянных параметров квантования и дискретизации может быть определена как:

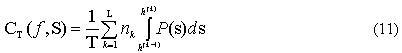
     Полученное выражение (10) для относительной избыточности кодирования позволяет дать достаточно простое физическое толкование этого понятия. Оно показывает, насколько среднее число двоичных символов в единицу времени на выходе кодера источника превышает минимально допустимое значение , необходимое для обеспечения заданной точности восстановления непрерывных сообщений. При этом отрицательные значения будут показывать, что кодирование f приводит к потерям информации относительно заданной точности .

Теорема 1. Теорема кодирования для непрерывных источников.

    1. Для каждого стационарного источника S и заданной точности восстановление непрерывных сообщений существует код f0, обеспечивающий сколь угодно малую неотрицательную относительную избыточность кодирования, то есть .