ПЕРЕДАЧА КОНФИДЕНЦИАЛЬНОЙ ИНФОРМАЦИИ ПО ВОЛОКОННО-ОПТИЧЕСКИМ ЛИНИЯМ СВЯЗИ, ЗАЩИЩЕННАЯ ОТ НЕСАНКЦИОНИРОВАННОГО ДОСТУПА - К.Е. Румянцев, И.Е. Хайров

где q и p - априорные вероятности посылки логических "0" и "1" соответственно; Р_лт и Р_пр - вероятность ложной тревоги и пропуска; P{j½n} - условные вероятности регистрации оптического излучения, зависящие от значения универсального параметра регистратора a. Обозначение [n_пор] означает ближайшее целое число в сторону увеличения.

Рассмотрим частный случай q=p=1/2.

Из формулы (2) следует

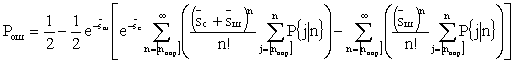.   (3)

Выражение (3) при q=p=1/2 определяет вероятность ошибки при различных энергиях сигнала и шума. Представляет интерес предельный случай, когда число шумовых фотонов достаточно мало [28], т.е. когда выполняется условие

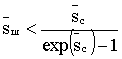                                                      (4)

На практике реален случай низкого уровня фона, когда отношение "шумовых" фотонов к "сигнальным" мало [27]. Это обусловлено тем, что: 1) относительное число "тепловых" фотонов быстро падает с ростом частоты и с уменьшением температуры; 2) при использовании направленных антенн можно добиться того, чтобы фотоны от посторонних источников не попадали на вход приемника; 3) сильным охлаждением приемника можно значительно ослабить уровень "темновых" электронов. Кроме того, этот случай позволяет оценить влияние квантовых эффектов, ограничивающих эффективность системы связи. При условии (4) n_пор в (3) становится равным нулю. При этом суммы условных вероятностей P{j|n} в (3) по всем  будут равны единице: .

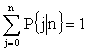Если положить , т.е. аддитивного шума нет, то из (3) следует (поскольку условие (4) также выполняется)  Из выражения видно, что при отсутствии аддитивного шума вероятность ошибки не зависит от параметров фотоэлектронного счетчика, а определяется только квантовыми эффектами. Действительно, при отсутствии аддитивного шума регистрация фотоэлектронным счетчиком хотя бы одного ФЭ говорит о наличии символа "1". Эта вероятность при конечных энергиях сигнала не обращается в нуль, что является следствием проявления квантовых эффектов [27]. При увеличении  (приближение к классическому случаю) видно, что  стремится к нулю.

Графики, позволяющие оценить эффективность приемника, работающего по правилу Зигерта-Котельникова для КИАМ системы связи в условиях действия пуассоновских шумов, приведены на рис. 1. Значения подсчитывались на ЭВМ для различных величин a с использованием формул (2) и (3). Сплошными линиями на рис. 1 построены зависимости в предположении отсутствия флуктуаций амплитуд ОИ, а пунктирными ¾ с флуктуациями.

Случай, при котором a=0, является идеальным и определяет предельное минимальное значение полной ошибки, которая только может быть достигнута.